

Next: Implementation in the acquisition
Up: Background
Previous: Atmosphere model
The atmospheric phase affecting the observations is given by:
Ideally one would like use 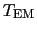 measured every second for each antenna, to
compute the corresponding
measured every second for each antenna, to
compute the corresponding 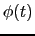 , and to correct the measured baseline
phases.
, and to correct the measured baseline
phases.
Practically this is not feasible, since 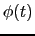 amounts to many turns,
and instrumental effects affect the measured
amounts to many turns,
and instrumental effects affect the measured 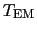 . The receiver gains, the
forward efficiencies vary with the source elevation. So when the antennas
are moved in elevation by more that a few degrees, like when switching
between observed sources, these effects spoil the measured
. The receiver gains, the
forward efficiencies vary with the source elevation. So when the antennas
are moved in elevation by more that a few degrees, like when switching
between observed sources, these effects spoil the measured 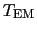 and
prevent the use of the derived pathlength values.
and
prevent the use of the derived pathlength values.
Instead we use a differential procedure: once the antennas track a given
source, one calibrates the atmosphere to calculate
 ,
, 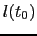 ,
and
,
and
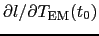 .
.
The relative change in total power is:
The
phase correction applied is then:
which we may rewrite as
The choice of
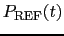 will be made in order to include as much as possible
all the slow effects that contribute to
will be made in order to include as much as possible
all the slow effects that contribute to
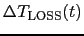 . It is not a
problem if long term atmospheric effects are also included in
. It is not a
problem if long term atmospheric effects are also included in
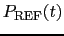 ;
these effects will not be removed by the radiometric phase correction, but
by the traditional phase referencing on a nearby calibrator.
;
these effects will not be removed by the radiometric phase correction, but
by the traditional phase referencing on a nearby calibrator.
Several choices of
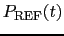 may be used:
may be used:
- Use for a given time interval (e.g. a scan of
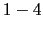 min. duration)
the average of
min. duration)
the average of 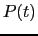 in the same interval. This ``minimal'' choice has
the advantage of correcting the amplitude of the decorrelation effect as
much as possible (of course decorrelation effects occurring inside an
elementary sampling interval, one second, will not be corrected; but this
may usually be neglected). The average phase should not be affected. This
is the scheme we plan to apply in quasi-real time in the correlators, to
the spectral line data.
in the same interval. This ``minimal'' choice has
the advantage of correcting the amplitude of the decorrelation effect as
much as possible (of course decorrelation effects occurring inside an
elementary sampling interval, one second, will not be corrected; but this
may usually be neglected). The average phase should not be affected. This
is the scheme we plan to apply in quasi-real time in the correlators, to
the spectral line data.
- Use, for a longer time scale (e.g. the on-source time between two
observations of the phase calibrator), a linear fit to the
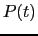 data as
the
data as
the
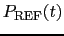 reference. This is basically the same choice, but additionnaly
allows for a linear drift of
reference. This is basically the same choice, but additionnaly
allows for a linear drift of
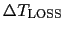 during the observation. This
choice is currently implemented in CLIC (see below).
during the observation. This
choice is currently implemented in CLIC (see below).
- Use a smooth curve approximation to
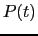 on a longer time scale
(one or several hours). This approximation should be different for the
source data and the phase calibrator data. This has not been really tried
yet.
on a longer time scale
(one or several hours). This approximation should be different for the
source data and the phase calibrator data. This has not been really tried
yet.
- Use a realistic model of the system noise as a function of azimut and
elevation, and other parameters: although some effects should be easily
calibrated out (e.g. by monitoring the temperature of the receiver
cabin), such a detailed knowledge of the ground noise properties of the
PdB antennas is difficult to reach, and not yet available.


Next: Implementation in the acquisition
Up: Background
Previous: Atmosphere model
Gildas manager
2014-07-01
![]() measured every second for each antenna, to
compute the corresponding
measured every second for each antenna, to
compute the corresponding ![]() , and to correct the measured baseline
phases.
, and to correct the measured baseline
phases.
![]() amounts to many turns,
and instrumental effects affect the measured
amounts to many turns,
and instrumental effects affect the measured ![]() . The receiver gains, the
forward efficiencies vary with the source elevation. So when the antennas
are moved in elevation by more that a few degrees, like when switching
between observed sources, these effects spoil the measured
. The receiver gains, the
forward efficiencies vary with the source elevation. So when the antennas
are moved in elevation by more that a few degrees, like when switching
between observed sources, these effects spoil the measured ![]() and
prevent the use of the derived pathlength values.
and
prevent the use of the derived pathlength values.
![]() ,
, ![]() ,
and
,
and
![]() .
.
![]() will be made in order to include as much as possible
all the slow effects that contribute to
will be made in order to include as much as possible
all the slow effects that contribute to
![]() . It is not a
problem if long term atmospheric effects are also included in
. It is not a
problem if long term atmospheric effects are also included in
![]() ;
these effects will not be removed by the radiometric phase correction, but
by the traditional phase referencing on a nearby calibrator.
;
these effects will not be removed by the radiometric phase correction, but
by the traditional phase referencing on a nearby calibrator.
![]() may be used:
may be used: