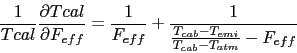


Next: Relative to
Up: Derivatives
Previous: Relative to
Contents
Again, from Eq. (30), assuming 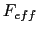 and
and 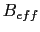 are independent,
are independent,
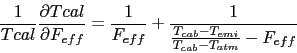 |
(44) |
which is of the order of 1.4 for the numerical values in Eq. (31). The
first term must be omitted if one assumes 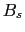 =
= 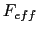 , and in this
case the derivative is of the order of 0.26.
, and in this
case the derivative is of the order of 0.26.
Gildas manager
2014-07-01
![]() and
and ![]() are independent,
are independent,