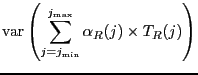 |
(14) | ||
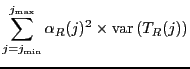 |
(15) | ||
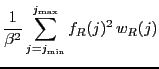 |
(16) |
![[*]](crossref.png) is derived from the general variance
property:
is derived from the general variance
property:
| (17) |
Finally from eqs. ![[*]](crossref.png) and
and ![[*]](crossref.png) , the resampled
channel weight is4:
, the resampled
channel weight is4:
|
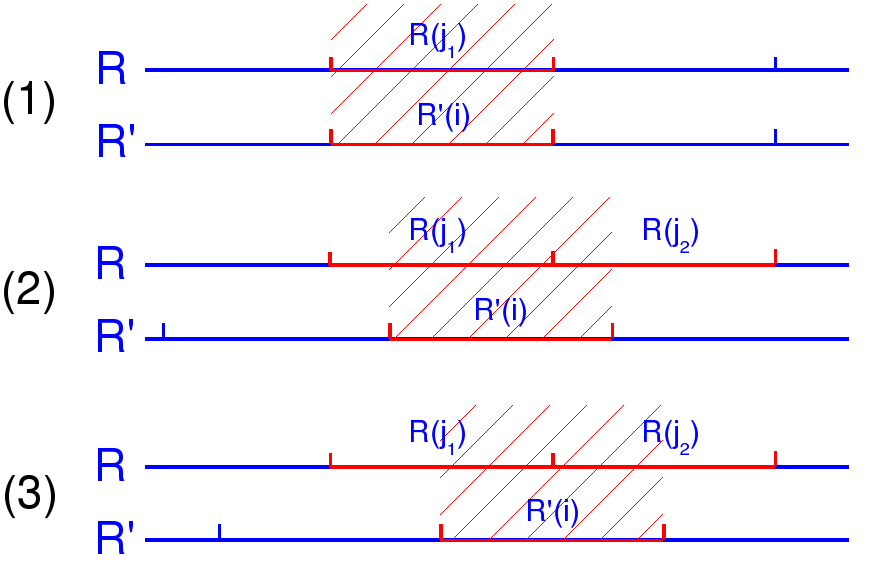
This relation has a non-intuitive effect on the resampled spectrum:
its weight is, in the general case, different from the original
one. Let's assume that the spectrum ![]() is resampled onto a spectrum
is resampled onto a spectrum
![]() with the same resolution but with a shifted value
with the same resolution but with a shifted value
![]() at reference channel (fig.
at reference channel (fig. ![[*]](crossref.png) ). In such a case, the
channel weight
). In such a case, the
channel weight ![]() we can deduce, and its associated
we can deduce, and its associated ![]() ,
are:
,
are:
| 1. |
|
|
|
| 2. |
|
|
|
| 3. |
|
|
|
This should be kept in mind when averaging e.g. two ![]() and
and ![]() spectra with same resolution but shifted X-axis. If a SIGMA
weighting is invoked, the average won't be found at the mean distance
of the two spectra even if their
spectra with same resolution but shifted X-axis. If a SIGMA
weighting is invoked, the average won't be found at the mean distance
of the two spectra even if their ![]() are equal!
are equal!
One should also take care that eq. ![[*]](crossref.png) assumes
uncorrelated input channels. Resampling a spectrum which
was already resampled (e.g.
assumes
uncorrelated input channels. Resampling a spectrum which
was already resampled (e.g.
![]() ) introduces
a correlation between more contiguous channels. In particular
this equation should not be used to compute the associated
weights.
) introduces
a correlation between more contiguous channels. In particular
this equation should not be used to compute the associated
weights.
The weight at eq. ![[*]](crossref.png) apply to the TIME and
SIGMA weighting, where the computations above have a physical
meaning and one can expect consistant values for integration time,
channel width and
apply to the TIME and
SIGMA weighting, where the computations above have a physical
meaning and one can expect consistant values for integration time,
channel width and ![]() . For the EQUAL weighting, user
expects the two input spectra to have the same weight whatever their
abscissa axis definition: this means that a re-EQUALization of
the channels must come after the resampling. The ad hoc
weighting is in this case:
. For the EQUAL weighting, user
expects the two input spectra to have the same weight whatever their
abscissa axis definition: this means that a re-EQUALization of
the channels must come after the resampling. The ad hoc
weighting is in this case:
![[*]](crossref.png) ) for a
new input spectrum, or any (possibly not constant) value for the
reentrant sum. This preserves a correct ponderation of the reentrant
sum in front of a new input spectrum.
) for a
new input spectrum, or any (possibly not constant) value for the
reentrant sum. This preserves a correct ponderation of the reentrant
sum in front of a new input spectrum.