


Next: Single-dish calibration in a
Up: IRAM Memo 2009-5 Comparison
Previous: Contents
Contents
Let 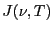 be the power radiated by a black-body at frequency
be the power radiated by a black-body at frequency 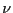 and temperature
and temperature 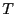 . It is always possible to define in a conventional way
a Rayleigh-Jeans temperature
. It is always possible to define in a conventional way
a Rayleigh-Jeans temperature
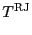 such as
such as
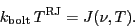 |
(1) |
It happens that
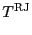 has a direct physical meaning, i.e.
has a direct physical meaning, i.e.
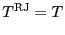 ,
when
,
when
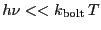 . However,
. However,
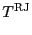 can always be defined (even when
can always be defined (even when
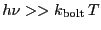 :
:
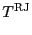 just loses its physical meaning. The advantage
of doing this is that all the equations of calibrations are considerably
simpler to write and to implement in source code using the conventional
Rayleigh-Jeans temperature than the black-body formula. The only constraint
is to remember to transform physical temperature (in particular hot and
cold load temperature) in conventional Rayleigh-Jeans temperature for all
the input parameters. This is what is done in GILDAS/TELCAL, in
ATM and thus in this memo.
just loses its physical meaning. The advantage
of doing this is that all the equations of calibrations are considerably
simpler to write and to implement in source code using the conventional
Rayleigh-Jeans temperature than the black-body formula. The only constraint
is to remember to transform physical temperature (in particular hot and
cold load temperature) in conventional Rayleigh-Jeans temperature for all
the input parameters. This is what is done in GILDAS/TELCAL, in
ATM and thus in this memo.
Gildas manager
2014-07-01
![]() be the power radiated by a black-body at frequency
be the power radiated by a black-body at frequency ![]() and temperature
and temperature ![]() . It is always possible to define in a conventional way
a Rayleigh-Jeans temperature
. It is always possible to define in a conventional way
a Rayleigh-Jeans temperature
![]() such as
such as