


Next: EKH vs shift-and-add restoration
Up: Mapping
Previous: Mapping
Contents
A bolometer measures other contributions (e.g. the atmospheric emission),
which usually domintes the measured signal. Moreover, MAMBO bolometers have
a finite time response. The strategy to map a source must take care of both
effects. One way is to wobble the secondary in the scanning direction. We
note that it is customary to scan in the azimuthal direction because this
allows to scan at nearly constant airmass (i.e. at constant elevation).
However, when mapping an elongated source (e.g. an edge-on galaxy disk),
the restoration algorithms work best when scanning along the smallest
source size. In addition, the observing mode (wobbling) introduces strong
boundary conditions, which in general implies that the whole array must
scan over the full source size. In addition, a portion of blanked sky
(typically 3 times the full width at half maximum of the telescope beam)
must be be observed to baseline the data.
In summary, if the PI wants to map a source of size
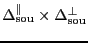 , the total scanned size will have to be
, the total scanned size will have to be
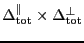 with
with
where
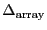 is the linear array size,
is the linear array size,
 is the wobbler throw
and
is the wobbler throw
and
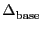 is the size of blanked sky used for baselining. The rows of
the map (i.e. the subscans) are scanned at constant velocity,
is the size of blanked sky used for baselining. The rows of
the map (i.e. the subscans) are scanned at constant velocity,
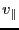 . The
size of the row will be
. The
size of the row will be
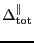 . Each row will be an independent
subscan of duration
. Each row will be an independent
subscan of duration
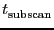 . The separation between two rows will be
. The separation between two rows will be
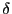 . If the area to be mapped is called
. If the area to be mapped is called
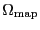 , the time to cover it
once is called
, the time to cover it
once is called
 and the number of subscans per coverage is called
and the number of subscans per coverage is called
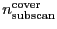 , the following relationships hold
, the following relationships hold
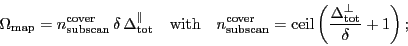 |
(12) |
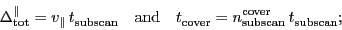 |
(13) |
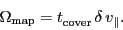 |
(14) |
Note that the grouping of the subscans in coverages is independent of the
grouping of the subscans in scans, e.g. the same scan can finish a
coverage of the source and start a new one.



Next: EKH vs shift-and-add restoration
Up: Mapping
Previous: Mapping
Contents
Gildas manager
2014-07-01
![]() , the total scanned size will have to be
, the total scanned size will have to be
![]() with
with