Decomposing the elapsed telescope time

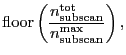
Next: OnOff Up: Generalities Previous: Estimator philosophy Contents

Decomposing the elapsed telescope time

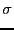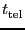If the PI wants to reach the same rms noise ( $\ensuremath{\sigma_\ensuremath{\mathrm{}}}$ ) on $\ensuremath{n_\ensuremath{\mathrm{source}}}$ sources (they must share the same calibrator sources), during a given elapsed telescope time ( $\ensuremath{t^\ensuremath{\mathrm{}}_\ensuremath{\mathrm{tel}}}$ ), we have

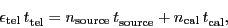$\begin{displaymath} \ensuremath{\epsilon_\ensuremath{\mathrm{tel}}}\, \ensurema... ...nsuremath{t^\ensuremath{\mathrm{}}_\ensuremath{\mathrm{cal}}}, \end{displaymath}$

(2)

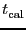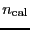where $\ensuremath{t^\ensuremath{\mathrm{}}_\ensuremath{\mathrm{cal}}}$ is the time required to acquire the calibration information and $\ensuremath{n_\ensuremath{\mathrm{cal}}}$ the number of such calibration suits.

The calibration time can be written as

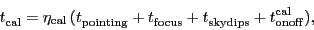$\begin{displaymath} \ensuremath{t^\ensuremath{\mathrm{}}_\ensuremath{\mathrm{ca... ...ath{t^\ensuremath{\mathrm{cal}}_\ensuremath{\mathrm{onoff}}}), \end{displaymath}$

(3)

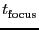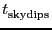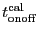where $\ensuremath{t^\ensuremath{\mathrm{}}_\ensuremath{\mathrm{pointing}}}$ , $\ensuremath{t^\ensuremath{\mathrm{}}_\ensuremath{\mathrm{focus}}}$ , $\ensuremath{t^\ensuremath{\mathrm{}}_\ensuremath{\mathrm{skydips}}}$ and $\ensuremath{t^\ensuremath{\mathrm{cal}}_\ensuremath{\mathrm{onoff}}}$ are respectively the typical times needed to perform a pointing, focus and skydip measurement and an OnOff measurement on a calibrator. 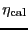$\ensuremath{\eta_\ensuremath{\mathrm{cal}}}$ is a multiplicative factor

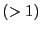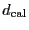which takes into account the time to slew to the pointing and/or focus source as well as the possible need to do such calibrations twice in a row. The number of such calibrations is dictated by the fact that the maximum duration between two such calibration suits must be $\ensuremath{d_\ensuremath{\mathrm{cal}}}$ . This gives

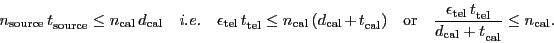$\begin{displaymath} \ensuremath{n_\ensuremath{\mathrm{source}}}\,\ensuremath{t^... ...{\mathrm{cal}}}} \le \ensuremath{n_\ensuremath{\mathrm{cal}}}. \end{displaymath}$

(4)

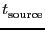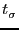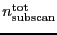The time spent per source ( $\ensuremath{t^\ensuremath{\mathrm{}}_\ensuremath{\mathrm{source}}}$ ) is linked to the integration time ( $\ensuremath{t^\ensuremath{\mathrm{}}_\ensuremath{\mathrm{\ensuremath{\sigma_\ensuremath{\mathrm{}}}}}}$ ) through the succession of $\ensuremath{n_\ensuremath{\mathrm{subscan}}^\ensuremath{\mathrm{tot}}}$ subscans, each subscan having an on-source integration time of $\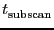ensuremath{t^\ensuremath{\mathrm{}}_\ensuremath{\mathrm{subscan}}}$ and an overhead time of $\ensuremath{t^\ensuremath{\mathrm{overhead}}_\ensuremath{\mathrm{subscan}}}$ . 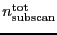The $\ensuremath{n_\ensuremath{\mathrm{subscan}}^\ensuremath{\mathrm{tot}}}$ subscans are grouped into scans, with an additional overhead time of $\ensuremath{t^\ensuremath{\mathrm{overhead}}_\ensuremath{\mathrm{scan}}}$ per scan. 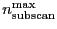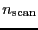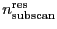If one scan can contain at most $\ensuremath{n_\ensuremath{\mathrm{subscan}}^\ensuremath{\mathrm{max}}}$ subscans, the number of scans ( $\ensuremath{n_\ensuremath{\mathrm{scan}}}$ ) and the residual number of subcans ( $\ensuremath{n_\ensuremath{\mathrm{subscan}}^\ensuremath{\mathrm{res}}}$ ) are computed through

$\displaystyle \ensuremath{n_\ensuremath{\mathrm{scan}}}$	$\textstyle =$	$\displaystyle \ensuremath{\mathrm{floor}}\ensuremath{\displaystyle\left( \frac{... ...suremath{n_\ensuremath{\mathrm{subscan}}^\ensuremath{\mathrm{max}}}} \right) },$	(5)
$\displaystyle \ensuremath{n_\ensuremath{\mathrm{subscan}}^\ensuremath{\mathrm{res}}}$	$\textstyle =$	$\displaystyle \ensuremath{n_\ensuremath{\mathrm{subscan}}^\ensuremath{\mathrm{t... ...{scan}}}\ensuremath{n_\ensuremath{\mathrm{subscan}}^\ensuremath{\mathrm{max}}}.$	(6)

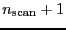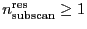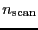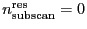We note that the actual number of scan is $\ensuremath{n_\ensuremath{\mathrm{scan}}}+1$ when $\ensuremath{n_\ensuremath{\mathrm{subscan}}^\ensuremath{\mathrm{res}}}\ge 1$ and $\ensuremath{n_\ensuremath{\mathrm{scan}}}$ when $\ensuremath{n_\ensuremath{\mathrm{subscan}}^\ensuremath{\mathrm{res}}}= 0$ . The time spent per source is thus given by

$\displaystyle \ensuremath{t^\ensuremath{\mathrm{}}_\ensuremath{\mathrm{scan}}}$	$\textstyle =$	$\displaystyle \ensuremath{n_\ensuremath{\mathrm{subscan}}^\ensuremath{\mathrm{m... ...}}) + \ensuremath{t^\ensuremath{\mathrm{overhead}}_\ensuremath{\mathrm{scan}}},$	(7)
$\displaystyle \ensuremath{t^\ensuremath{\mathrm{}}_\ensuremath{\mathrm{source}}}$	$\textstyle =$	$\displaystyle \ensuremath{n_\ensuremath{\mathrm{scan}}}\,\ensuremath{t^\ensurem... ...uremath{t^\ensuremath{\mathrm{overhead}}_\ensuremath{\mathrm{scan}}} \right] }.$	(8)

Next: OnOff Up: Generalities Previous: Estimator philosophy Contents

Gildas manager 2014-07-01