System temperature

The system temperature is a summary of the noise added by the system. This noise comes from 1) the receiver and the optics, 2) the emission of the sky, and 3) the emission picked up by the secondary side lobes of the telescope. It is usual to approximate it (in the 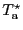scale) with

$$\ensuremath{T_\ensuremath{\mathrm{sys}}}= \frac{\ensuremath... ...hrm{cab}}}+\ensuremath{T_\ensuremath{\mathrm{rec}}} \right] },$$ (3)

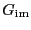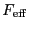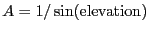where is the receiver image gain, the telescope forward efficiency, $\ensuremath{A}= 1/\sin(\ensuremath{\mathrm{elevation}})$ the airmass, 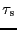the atmospheric opacity in the signal band, 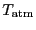the mean physical atmospheric temperature, 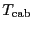the ambient temperature in the receiver cabine and 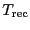the noise equivalent temperature of the receiver and the optics. All those parameters are easily measured, except 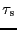, which is depends on the amount of water vapor in the atmosphere and which is estimated by complex atmospheric models.