Next: About this document ... Up: IRAM Memo 2009-1 IRAM-30m Previous: On-The-Fly Contents

Optimal number of ON per OFF measurements

This section is just a reformulation of the original demonstration by Ball (1976).

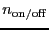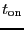Let's assume that we are measuring $\ensuremath{n_\ensuremath{\mathrm{on/off}}}$ independent on-positions for a single off. The same integration time ( $\ensuremath{t_\ensuremath{\mathrm{on}}}$ ) is spent on each on-position and the off integration time is

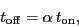$\begin{displaymath} \ensuremath{t_\ensuremath{\mathrm{off}}}= \alpha \, \ensuremath{t_\ensuremath{\mathrm{on}}}, \end{displaymath}$

(53)

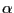where $\alpha$ can be varied. Using eq.

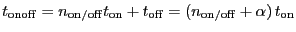and $\ensuremath{t_\ensuremath{\mathrm{onoff}}} = \ensuremath{n_\ensuremath{\mathrm{... ..._\ensuremath{\mathrm{on/off}}}+\alpha)\,\ensuremath{t_\ensuremath{\mathrm{on}}}$ , it can be shown than

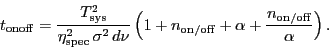$\begin{displaymath} \ensuremath{t_\ensuremath{\mathrm{onoff}}}= \frac{\ensurema... ...ensuremath{n_\ensuremath{\mathrm{on/off}}}}{\alpha} \right) }. \end{displaymath}$

(54)

Differenciating with respect to 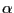$\alpha$ , we obtain

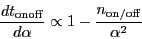$\begin{displaymath} \frac{d\ensuremath{t_\ensuremath{\mathrm{onoff}}}}{d\alpha}... ...1-\frac{\ensuremath{n_\ensuremath{\mathrm{on/off}}}}{\alpha^2} \end{displaymath}$

(55)

Setting the result to zero then gives that the minimum elapsed time to reach a given rms noise is obtained for

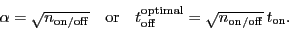$\begin{displaymath} \alpha = \sqrt{\ensuremath{n_\ensuremath{\mathrm{on/off}}}}... ...\mathrm{on/off}}}} \, \ensuremath{t_\ensuremath{\mathrm{on}}}. \end{displaymath}$

(56)

Gildas manager 2014-07-01