![[*]](crossref.png) and
and ![[*]](crossref.png) , we obtain
, we obtain
Using this equation, we start to compute
Eq.
![[*]](crossref.png) ensures that
ensures that
![[*]](crossref.png) is enforced.
is enforced.
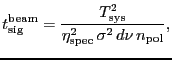 |
(39) | ||
| (40) | |||
| (41) |
| (42) | |||
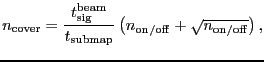 |
(43) | ||
| (44) | |||
| (45) |
-
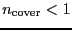 . This means that either the user tries to cover a too
large sky area in the given telescope elasped time (sensitivity
estimation) or the telescope need a minimum time to cover
. This means that either the user tries to cover a too
large sky area in the given telescope elasped time (sensitivity
estimation) or the telescope need a minimum time to cover
 at
the maximum velocity possible with the telescope and this minimum time
implies a more sensitive observation than requested by the user (time
estimation).
at
the maximum velocity possible with the telescope and this minimum time
implies a more sensitive observation than requested by the user (time
estimation).
-
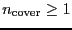 .
.
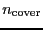 will generally not be an integer, we can
think to decrease
will generally not be an integer, we can
think to decrease
 from
from
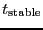 to obtain an integer
value. However, this must be done at constant
to obtain an integer
value. However, this must be done at constant
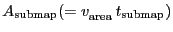 . Decreasing
. Decreasing
 thus implies increasing
thus implies increasing
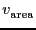 .
It is not clear that this is possible because of the constraint
.
It is not clear that this is possible because of the constraint
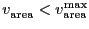 . Another way to deal with this is to keep
. Another way to deal with this is to keep
 to
its maximum value and to adjust
to
its maximum value and to adjust
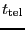 (sensitivity estimation) or
(sensitivity estimation) or
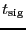 and thus
and thus
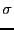 (time estimation) to obtain an integer value
of
(time estimation) to obtain an integer value
of
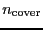 . However, this implies a change in the wishes of the user.
The program can not make such a decision alone and we will only warn
the user. Indeed, the worst case is when
. However, this implies a change in the wishes of the user.
The program can not make such a decision alone and we will only warn
the user. Indeed, the worst case is when
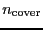 is changing from 1
to 2 because this can decrease the sensitivity by a factor 1.4
(sensitivity estimation) or double the elapsed telescope time (time
estimation). The larger the value of
is changing from 1
to 2 because this can decrease the sensitivity by a factor 1.4
(sensitivity estimation) or double the elapsed telescope time (time
estimation). The larger the value of
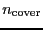 the less harm it is to
enforce the integer character of
the less harm it is to
enforce the integer character of
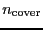 .
.